Comment adapter les quantités d’une recette ?
Adapter les quantités d’une recette en pâtisserie est une compétence essentielle pour tout pâtissier. Comme dans le métier, nous sommes souvent amenés à recalculer nos recettes, soit à augmenter les quantités, soit à les réduire, nous devons pouvoir rapidement effectuer les bons calculs. En pâtisserie, chaque gramme compte pour maintenir l’équilibre des saveurs et des textures. Une erreur de quantité peut être catastrophique au visuel et au goût ! C’est pourquoi, savoir ajuster les ingrédients avec précision est crucial pour garantir le succès de vos desserts.
Même si vous n’êtes pas très à l’aise avec les maths et que vous suivez les conseils pratiques que je vous donnes dans cet article, vous ne devriez plus avoir de problèmes de conversions de recette. Mais il faudra tout de même s’exercer pour bien assimiler les méthodes de calculs.
Temps de lecture : 4 minutes
Calculer les quantités d’une recette avec le produit en croix
Le produit en croix est une méthode simple et efficace utilisée pour résoudre des problèmes de proportionnalité. Cette méthode permet de trouver facilement une valeur inconnue (x) dans une proportion donnée de A, B et C.
Créer un tableau de proportionnalité
Pour faire vraiment simple, si vous avez des difficultés en calcul mental ou a visualisé le calcul, le mieux est de poser les grammages de la recette dans un tableau.
Par exemple, pour la meringue italienne la recette indique 145 g de blancs d’œufs, 290 g de sucre blanc et 96,6 g d’eau. Or dans votre frigo, vous constatez que vous possédez seulement de 90 g de blanc d’œufs. Voyons, comment calculer les proportions des autres ingrédients dans le tableau ci-dessous :
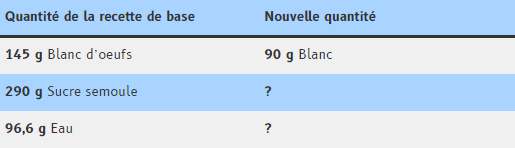
Il faut établir le produit en croix. Tracez visuellement une croix entre les deux quantités de blancs et le sucre.
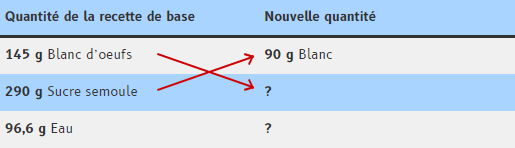
On peut écrire cette proportion ainsi :
145 g blancs
290 g sucre
90 g blancs
X sucre
On multiplie en diagonale suivant la croix qu’on a tracé pour trouver X soit la nouvelle quantité sucre :
X = 290 x 90 = 26100
Ensuite de ce produit, on le divise toujours par la quantité de blanc de la recette de base :
X = 26100 / 145 = 180
Ce qui nous donne comme nouvelle quantité de sucre 180 g.
Le calcul est le même pour trouver la quantité d’eau adaptée :
Eau : X = 96,6 x 90 / 145 = 59,95
Résultat du produit en croix :
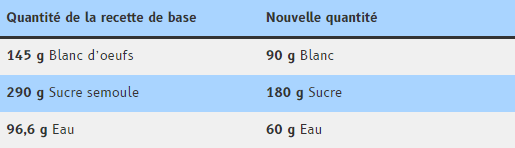
Pour éviter de se tromper :
Quelque soit la recette, prenez toujours comme base de calcul les quantités de l’ingrédient principal que vous avez changé dès le départ. Comme pour ici, pour trouver la nouvelle dose de sucre et d’eau j’ai fais mon calcul sur la base des blancs d’œufs.
Bon à vrai dire, la meringue est une recette ultra simple puisqu’il n’y a pas forcément besoin de faire le produit en croix. Sachez qu’il faut juste doubler la dose de sucre par rapport au blanc. Et pour l’eau, c’est toujours un tiers du sucre. Voilà, tout simplement !
Le produit en croix est une valeur sûre pour recalculer les quantités d’une recettes, à condition de multiplier et diviser les bons nombres. Malgré tout, la méthode s’avère long à appliquer si vous souhaitez adapter plusieurs recettes en même temps, comme par exemple tous les éléments que composent un entremet (biscuit, insert, mousse et glaçage). Et de plus, vous pouvez vous emmêler les pinceaux avec les multiples croisement de calculs, ce qui risque de fausser toutes vos pesées. L’autre méthode pour calculer les quantités d’une recette rapidement est d’utiliser le coefficient multiplicateur.
Trouver le coefficient multiplicateur
Le coefficient multiplicateur est un nombre par lequel vous multipliez les quantités des ingrédients d’une recette pour obtenir une nouvelle quantité souhaitée. Il permet de maintenir les proportions exactes des ingrédients, garantissant ainsi que la texture, la saveur et l’apparence du produit final restent constants.
Adapter les quantités d’une recette avec le coefficient multiplicateur ?
Une règle simple à appliquer : pour commencer, il faut déterminer la quantité initiale et la quantité désirée. A partir de là, vous calculez le coefficient multiplicateur.
Prenons un exemple : adapter les quantités d’une recette de crème pâtissière
Supposons que vous avez 550 g de lait et que vous souhaitez impérative tout utiliser avant sa date de péremption. La recette initiale de la crème pâtissière est :
Vous avez les deux informations essentielles pour connaitre le coefficient, soit :
– La quantité de base de la recette = 300 g
– La quantité souhaitée = 550 g
La règle de calcul est le suivant :
Divisez toujours la nouvelle quantité souhaitée par la quantité initiale.
Coefficient multiplicateur :
Quantité souhaitée
Quantité initiale
550
300
1,833
Enfin, vous n’avez plus qu’à appliquer ce coefficient à chaque ingrédient de la recette.
| Ingrédients | Quantité de base x Coefficient multiplicateur | Nouvelle quantité |
|---|---|---|
| Lait | 300 x 1,833 | 550 |
| Jaunes d’œufs | 120 x 1,833 | 220 |
| Poudre à crème | 20 x 1,833 | 37 |
| Sucre | 96 x 1,833 | 176 |
Pour vérifier que le coefficient est correcte, divisez-le par la quantité souhaitée. Normalement, vous devriez retomber sur la quantité initiale de la recette !
Comme ceci : 550 / 1.833 = 300
Toutefois, petit point important sur les coefficients à chiffre répété après la virgule. Pour l’exemple ci-dessus, j’ai coupé mon coefficient de 1,8333333 à 1,833, afin d’obtenir 550, ou pour être exacte 549,9 que j’ai arrondi. Dans le cas où j’ai utilisé seulement deux chiffres après la virgule, soit 1,83 ; le résultat était légèrement différent. Au lieu de 550 voulu, j’obtenais 549 = 1,83 x 300.
Cela fait une petite différence, mais en pâtisserie le moindre changement de proportion peut avoir une incidence sur le produit final. Par conséquent, faites attention en utilisant le coefficient multiplicateur. Ca vaut aussi lorsque vous pensez bien faire en arrondissant le coefficient. Comme par exemple, si vous arrondissez 1,833 par 2, vous verrez que la quantité désirée en est complètement changé.
Comment vérifier les calculs ?
Entrainez vous à trouver le coefficient multiplicateur. Ensuite, après réajustement des quantités de vos recettes, vérifiez que celles-ci soient logiques. Je m’explique avec une petite anecdote sur ce sujet, un de mes élèves devait réduire les pesées d’une meringue italienne. Comme évoqué plus haut, le principe de la recette est toujours constituée de la même manière : une dose de blanc d’œuf (ex : 50 g), une double dose de sucre par rapport au blanc (= 100 g) et un tiers en eau du sucre (= 33 g). Il se trouve que l’élève en question avait calculé une quantité de sucre presque égale au poids des blancs d’œufs (pour 35 g de blanc, il avait 40 g de sucre, au lieu de 70 g). Son coefficient multiplicateur n’était pas bon. Mais, il ne voyait pas l’incohérence des quantités par rapport à la recette de base.
La logique du calcul, le coefficient multiplicateur doit être :
En dessous de < 1 si vous devez réduire les quantités
Exemple : Pour la crème pâtissière ci-dessus, je souhaite utiliser seulement 105 g de lait, à la place des 300 g donnée sur la recette. Mon coefficient multiplicateur est donc : 105 / 300 = 0,35.
| Quantité de base | Ingrédients | Quantité désirée | Coefficient multiplicateur |
|---|---|---|---|
| 300 | Lait | 105 | 0,35 |
| 120 | Jaunes d’œufs | 42 | |
| 20 | Poudre à crème | 7 | |
| 96 | Sucre | 33,6 |
Au dessus de > 1 si vous devez augmenter les quantités
Exemple : De la même manière, je veux cuire plus de crème pâtissière, car j’ai 330 g de jaunes d’œufs à passer. Le calcul est le suivant pour obtenir le coefficient : 330 / 120 = 2,75.
| Quantité de base | Ingrédients | Quantité désirée | Coefficient multiplicateur |
|---|---|---|---|
| 300 | Lait | 825 | |
| 120 | Jaunes d’œufs | 330 | 2,75 |
| 20 | Poudre à crème | 55 | |
| 96 | Sucre | 264 |
En résumé, pour adapter les quantités d’une recette, lorsque vous réduisez la dose de chaque ingrédient, vous ne devez pas vous retrouver avec un résultat plus élevé que la quantité initiale. Si, c’est le cas, reprenez vos calculs, il y a une erreur. Pareil, si vous voulez augmenter les proportions de la recette. Les nombres trouvés doivent être supérieurs à la recette de base. En cas de doute, pensez également que le produit en croix est une valeur sûre pour vérifier et corriger vos calculs.

Laisser un commentaire